14 の側面があり、曲線が多く、隙間や重なりなく表面を覆うことができるものは何ですか? それは不思議ではありません – それは「アインシュタインの吸血鬼」です。
3月に、デヴィッド・スミスという名の元版画家が科学者によって驚くべき発見をした。 数学。 見つかった 繰り返しなく全面を塗りつぶせる13面体。 なんとなくフェドーラ帽のような形をしていることから「帽子」と呼ばれるこの帽子は、世界中の数学者による数十年にわたる狩猟の集大成でした。
1961年以降 数学者たちは不思議に思った そういうフォーマットが存在できれば。 まず、数学者は、決して繰り返されないパターンを作成しながらつなぎ合わせることができる 20,426 個の形状のセットを発見しました (繰り返しパターンを作成するキッチンの床のタイルとは異なります)。 最終的に、数学者は、決して繰り返されないタイリングを作成できる 104 個の図形のセットを発見しました。
その後 1970 年に、物理学者でノーベル賞受賞者のロジャー ペンローズは、一緒になって非反復タイリングを作成する 2 つの形状を発見しました。 それ以来何十年もの間、数学者たちは同じトリックを 1 つの形状だけで実行できるのではないかと考え続けました。 この半ば伝説的な形状は、正式には非周期的単層として知られ、ドイツ語で「1 つの石」を意味する「アインシュタイン」として知られるようになりました。
しかし、スミスがアインシュタインの作品を発見したことで大騒ぎになったにもかかわらず、軟膏の中に小さなハエがいた。 繰り返しのないタイリングを作成するには、「帽子」をその鏡像と連動させる必要がありました。 技術的には、それは同じ形で、反転しただけですが、スミスは実際には本物のアインシュタインを見つけなかったと主張する人もいます。
しかし今、スミスと彼の同僚はそれらの反対意見を解消しました。彼らは、ループや反転をせずに表面をコーティングできる形状を発見しました。 彼らは5月28日にプレプリントデータベースに掲載された論文で新しい形状について説明した arXiv、ただしまだ査読は受けていません。
チームは、自分の反射を見ることができないため鏡を必要としない吸血鬼に敬意を表して、彼らのフォームを「スペクター」と名付けました。
共著者のジョセフ・サミュエル・マイヤーズは、「平面タイルでは、タイルが反射するのはごく普通のことですが、非周期的な単層ハットには平面タイルの反射が必要であるという事実に不満を抱く人もいます。」と書いています。 マストドン。 「私たちの新しい印刷物では、アインシュタイン吸血鬼の最初の例であるスペクターを紹介します。反射のない非周期的な平面に汚れた単層です。」
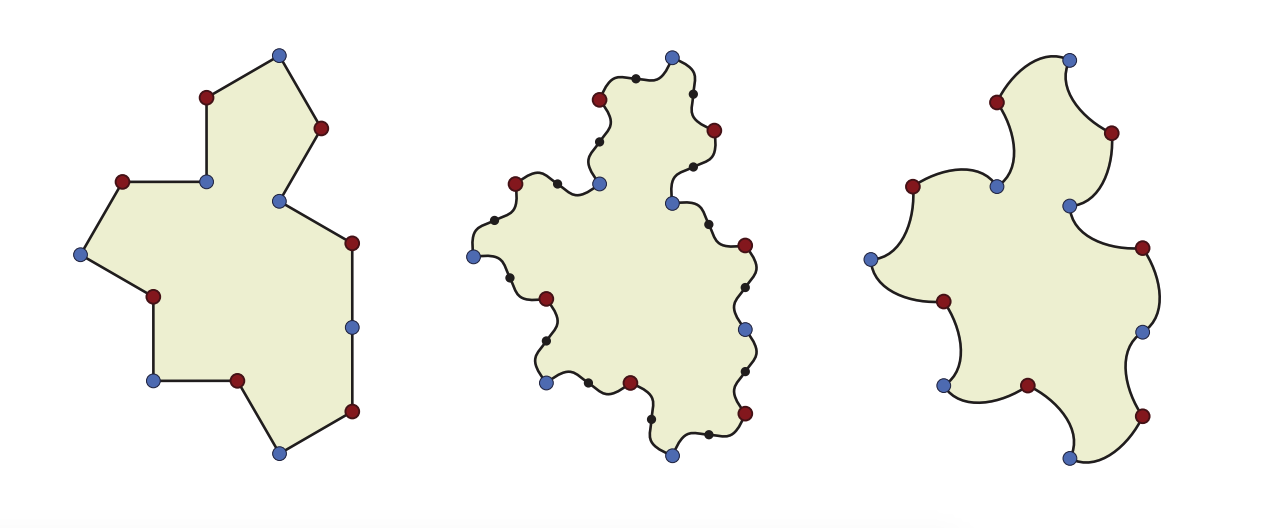
幽霊のような人物を見つけるために、チームは元の「帽子」の人物から始めて、それに追加の側面を追加しました。 この新しい形状には依然として完全な鏡像が必要でしたが、研究者らは、14 角形の直線エッジを曲線エッジに変えることで、鏡像を使わずに 1 つの形状だけで作業できることを発見しました。
「アマチュア主催者。ビールの伝道者になりたい。一般的なウェブファン。認定インターネット忍者。熱心な読者。」
More Stories
古いハッブル宇宙望遠鏡が故障から復活
アルパカのセックスはあなたが思っているよりも奇妙です
科学者たちは火星の太陽嵐に備えている